Zufallsvariablen
Häufig sind Ereignisse mit gewissen Zahlenwerten verbunden.
Beispielsweise ist die Augensumme beim zweimaligen Würfeln ein solcher Zahlenwert
und das Ereignis "Augensumme 5" wird durch E={(1,4), (2,3), (3,2), (4,1)} realisiert.
In dem Zusammenhang bezeichnet man die Augensumme als eine Zufallsvariable,
die die Werte 2 bis 12 annehmen kann.
Zufallsvariablen werden üblicherweise mit großen Buchstaben wie X, Y usw. bezeichnet.
Die Wahrscheinlichkeit dafür, dass eine Zufallsvariable X den Wert k annimmt notiert man als P(X=k).
Beispiel 1 für eine Zufallsvariable
Angenommen eine Münze werde 10mal geworfen. Gefragt wird nach der Wahrscheinlichkeit dafür,
dass genau 4mal Kopf erscheint. Hier können wir die "Anzahl Kopf" als Zufallsvariable X ansetzen.
X kann dann die Werte 0 bis 10 annehmen, denn bei 10 Würfen kann "Kopf" 0mal, 1mal, 2mal, ... 10mal vorkommen.
P(X=4) ist dann die Wahrscheinlichkeit dafür, dass bei 10 Würfen "Kopf" genau 4mal vorkommt
(wie man diese konkret berechnet sehen wir später).
Beispiel 2 für eine Zufallsvariable
Bei einer Tombola gibt es drei Arten von Gewinnen. Zeigt ein Los ein Sternchen, so
gewinnt man 5 €, zeigt es einen Kreis, so gewinnt man 2 € und bei einem Dreieck gewinnt man 1 €.
Wenn es nun um die Wahrscheinlichkeit für "irgendeinen" Gewinn geht, ist es nahe liegend,
diesen als Zufallsvariable X zu verwenden. X kann die Werte 0, 1, 2 oder 5 annehmen.
Beachten Sie, dass die 0 hier nicht vergessen werden darf, denn es gibt ja auch eine Wahrscheinlichkeit
dafür, dass man nichts gewinnt.
P(X=5) ist dann die Wahrscheinlichkeit dafür, dass man den Hauptgewinn gezogen hat.
Rechenbeispiel 1
Eine Urne enthält fünf weiße und drei rote Kugeln. Es wird dreimal mit Zurücklegen gezogen.
Bestimmen Sie die Wahrscheinlichkeiten dafür, dass die Ziehung keine, eine, zwei oder drei rote Kugeln enthält.
Lösung
Es sei X die Anzahl der roten Kugeln. X=0, also "keine rote Kugel", wird durch E0={(w,w,w)} realisiert.
Somit ist P(X=0) = P(E0) = (5/8)3 ≈ 0,244 = 24,4%.
X=1, d.h. "eine rote Kugel", wird realisiert durch E1={(r,w,w), (w,r,w), (w,w,r)}, also gilt
P(X=1) = P(E1) = 3·(5/8)2·3/8 ≈ 0,439 = 43,9%.
Die Ereignismengen zu X=2 und X=3 sind E2={(r,r,w), (r,w,r), (w,r,r)} und E3={ (r,r,r)}.
Entsprechend gilt für die Wahrscheinlichkeiten:
P(X=2) = 3·5/8·(3/8)2 ≈ 0,264 = 26,4% und
P(X=3) = (3/8)3 ≈ 0,053 = 5,3%.
Rechenbeispiel 2
Einem Kartenspiel mit 32 Karten werden nacheinander drei Karten ohne Zurücklegen entnommen.
Bestimmen Sie die Wahrscheinlichkeiten dafür, dass die Ziehung keine, eine, zwei oder drei Bildkarten (Bube, Dame oder König) enthält.
Lösung
Es sei X die Anzahl der Bildkarten. Dann gilt:
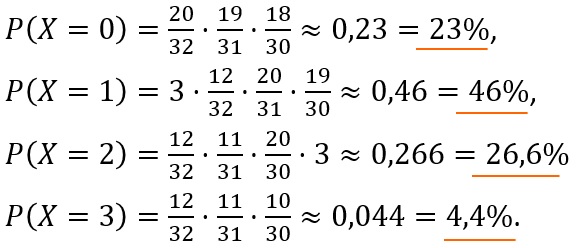
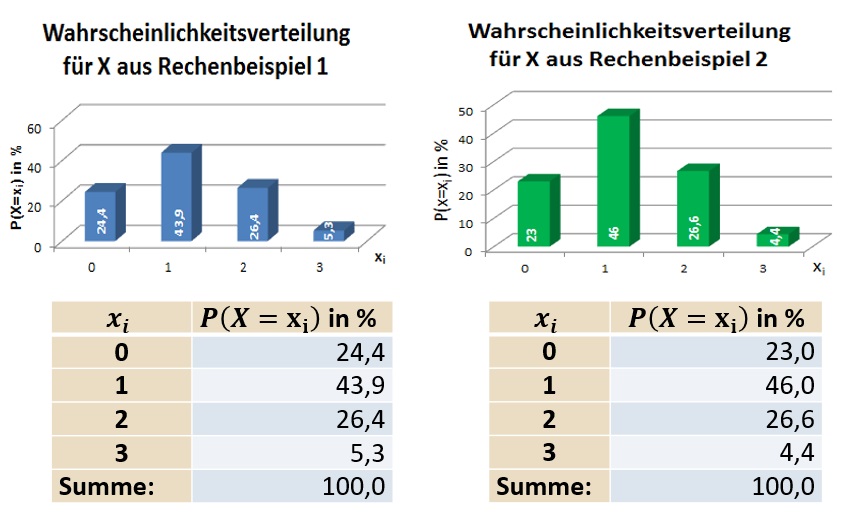
Spricht man von der Verteilung einer Zufallsvariablen X, so meint man damit die Gesamtheit aller Wahrscheinlichkeiten, mit denen die einzelnen Werte von X angenommen werden. Wahrscheinlichkeitsverteilungen werden häufig in Tabellen oder Histogrammen dargestellt.
| Downloads |
PowerPoint